Review of error calibration methods for ultra short baseline underwater acoustic positioning system

I. Introduction

Ultra short baseline underwater acoustic positioning system (USBL) displays the location of underwater targets in real time by means of data and graphics. It is a kind of underwater acoustic positioning system. It was developed in the 1970s and has the advantages of small array size, convenient installation and accurate measurement. Foreign (USBL) technology development is relatively mature, some companies have launched relatively mature products, so we can learn the international research progress in underwater acoustic location technology through the successful development of relevant products abroad. At the same time, due to foreign technology blockade and some historical reasons, the development of the domestic USBL is late, but there are still relevant units are actively studying the domestic ultra short baseline positioning system. In this paper, the progress of the ultra short baseline calibration methods at home and abroad is summarized.

Two, USBL composition and positioning principle

The ultra short baseline underwater acoustic positioning system integrates surface Marine equipment and transponder (see Figure 1). The basic unit of the former includes three parts: signal processing unit, acoustic energy exchanger array and peripheral auxiliary sensor. In applications, the acoustic transducer array is often fixed to the bottom or side of the vessel. The transponder needs to be set up on the underwater mobile carrier, if the synchronous clock trigger working mode, also need to connect the synchronous clock, to the water to transmit and receive the corresponding signal, transmission of mutual communication data, the range of directional radiation sound wave is hemispherical, no matter what kind of depth underwater and tilt Angle, will not hinder the normal operation of ultra-short baseline underwater acoustic positioning system.

The location of underwater target is determined by the arrival location and distance of the measured signal. The phase difference between the receiving array elements is used to complete the task of direction finding. The four matrix units of the ultra-short baseline matrix are set to form a left-handed coordinate system of the matrix, in which the origin coordinate is the center of the matrix O, the matrix elements 1 and 3 are distributed on the X-axis, and the matrix elements 2 and 4 are arranged on the Y-axis, and the distance between the matrix elements is D (refers to the spacing between the 1 and 3 matrix elements and the spacing between the 2 and 4 matrix elements). As shown in Figure 2:

Figure 2. Positioning principle diagram of ultra-short baseline underwater acoustic positioning system

In Figure 2, the position of the target to be determined is S, the target diameter vector is O -- S, α=[αxαyαz]' is represented by the directional angular vector, and the skew distance of the target is R. Assuming that the array size is small relative to the skew distance of the target, the plane wave approximation method is used to obtain the following formula:

Where c is the speed of sound in water, and τ13 and τ24 are 1, 3 and 2, 4 matrix, respectively. Due to different speed, transmission distance and different time, each signal has different delay phenomena, that is, delay difference of received signal, and the symbol of cos (αz) is determined from the prior information.

png is the directional angular vector of the geodetic coordinate system with the center of the matrix taken from the incident sound line and the origin. It can be obtained from the coordinate rotation theory:

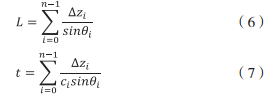
png is the rotation matrix from the carrier coordinate system to geodetic coordinate system, and image.png is the rotation matrix from the matrix coordinate system to the carrier coordinate system.

When the slant distance R is known, the geodetic coordinates with the matrix center as the origin can be obtained

The target position coordinate under the system is Rcos (image.png), where =[βx βy βz]'.

Three, the principle of sound line correction

Each layer is approximately composed of constant sound velocity. In other words, the distribution form of continuous changes in sound velocity is decomposed into the sound velocity distribution of the same sound velocity layer in each layer, and the actual sound track is represented by broken line approximation. The schematic diagram of sound velocity propagation track is shown in Figure 3.

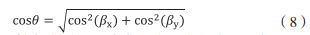
FIG. 3 Schematic diagram of sound velocity propagation track

The vertical depth from the water surface to the underwater target is divided into N layers, and each layer is equal in depth, propagates with constant sound velocity, and the sound velocity track is broken line. Then the acoustic track diagram is used to calculate the horizontal distance ∆xi and ∆ti, ∆Zi of each layer as the depth value of each layer, where Z0=Z1...... Zi, i= (0,1,2... ,N).

In layered media, ray acoustics follows Snell rate.

Where, C0 and θ0 are the initial sound velocity and initial grazing Angle, Ci is the sound velocity at layer i, and θi is the grazing Angle at the boundary of layer i. The total acoustic line travel L and the single harmonic line time t is equal to the superposition of ∆L and ∆t at N layers, so

In addition, the total time t required for the underwater acoustic signal to start from the underwater target S and propagate to the receiver array O. The measurement method can be either response mode or synchronous mode. Based on the system's measuability of the depth of the underwater target, the underwater target S is stratified until it reaches the end layer. Equations (5) and (7) were used to invert θ0, based on C (i i=0,1,2,... N), the required values θ (i i=0,1,2... N), then θ0 and Ci (i=0,1,2... can be obtained by formula (5). N), then, substitute into formula (7), synthesize the whole solution equation, it seems that there is only an unknown term θ0, because the whole formula requires complex calculation steps, it is difficult to calculate θ0 directly, so, in practical engineering applications, usually using programming, through the application of "pinch method" to obtain the initial grazing Angle θ0.

Three, the sound line bending correction method

Due to the non-uniform medium, it is easy to cause the bending and deformation of the sound line, which affects the accurate positioning of the USBL system. Therefore, it is necessary to correct the sound line. Different from the long baseline positioning system, the method of correcting the bending error of the ultra-short baseline needs to correct both distance and Angle.

(I) Distance correction method

The direction Angle cosine vector cos (image.png) of the incident sound line and the geodetic coordinate system with the center of the array as the origin can be calculated, and the Angle cosine of the incident sound line and the horizontal plane in the geodetic coordinate system with the center of the array as the origin can be calculated as:

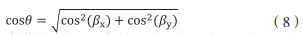
Where θ is the grazing Angle of the horizontal plane when the incident acoustic line reaches the geodetic coordinate system with the matrix center as the origin. In the case of no inversion, under the condition that the stratified distribution of sound velocity, the depth of transmitting point and receiving point are known, the sound track starting from the sound source and the linear slant distance R between transmitting and receiving signals can be backderived from the ray acoustic theory to correct the positioning distance. When an error in the grazing Angle θ is found, the horizontal distance between the transmitter and the receiver can be determined simply by searching the perimeter of θ in a small area.

(2) Direction Angle correction method

Suppose that the direction angular vector of the line between the receiver and the receiver and the geodetic coordinate system with the array center as the origin is =[δx δy δz]', then the coordinates of the target in the geodetic coordinate system with the array center as the origin are:

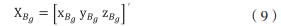
The geodetic coordinate system with the matrix center as the origin is set as O-Neu coordinate system, where O is the matrix center. G is set as the target position G1 of the uncorrected directional Angle, whose projection on the horizontal plane is G1', and the horizontal distance between G1' and the center of the matrix is r1, then the included Angle with the horizontal plane NOE is θ. Set the true position of the target as G, its projection on the horizontal plane NOE as G', the horizontal distance between G and the center point of the array as r, and the included Angle between g and the horizontal plane NOE as, and image.png. The position of the sound line projection on the horizontal plane does not change due to the bending of the sound line, so the projection of G1 and G on the horizontal plane is the same line, OG1G1' coincides with OGG'. The schematic diagram of azimuth correction is shown in the figure:

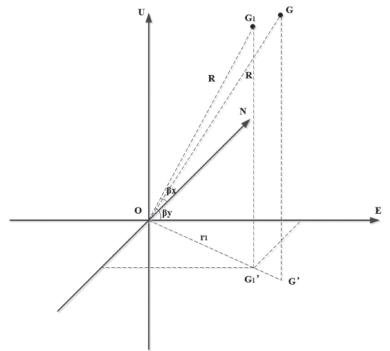
FIG. 4 Schematic diagram of directional Angle correction

Therefore, according to the geometric relation, it can be obtained:

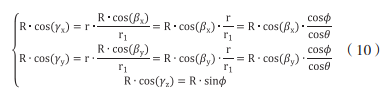
The above is the USBL positioning formula after sound line bending correction.

Iv. Research status of USBL error calibration technology

(I) Foreign research status of USBL installation error calibration technology

In 1997, Jan of IFREMER, a French Institute for Marine Development, proposed a circular calculation of mismatch matrix. In view of the ultra-short baseline positioning formula, the mismatch matrix was set as the rotation matrix obtained from the installation rotation deviation. In the multi-point positioning of the same target, the positioning point was converging through circular adjustment of the mismatch matrix. It eliminates the calibration of installation displacement deviation, but provides an idea to solve the calibration problem. In addition, French engineer Opderbecke calibrated the Angle deviation and proposed a new USBL positioning model.

From 1997 to 2010, it has been possible to use GPS technology and sound velocity theory to realize the centimeter-scale location of ocean floor. Opderbecke proposed that the surface ship travel along any track and collect data in multiple directions, taking the fixed underwater target as reference. In 2002, Faugstadmo et al. proposed to calibrate the angular deviation by using the running track of a survey ship with a series of shapes such as a circle. To improve calibration accuracy, Faugstadmo et al. added a dynamic positioning device to the calibration scheme. In 2003, three USBL installation and calibration papers published by Philips in the United States did not include the calibration algorithm and formula, but followed the calculation strategy proposed by Jan of the Institute of Marine Exploitation in France, specifically identifying the same underwater positioning target and marking its installation displacement deviation and installation rotation deviation. In addition, J. D. Powell et al., Stanford University, used spatial Angle measurements in the calibration of array and hull deviations. Pettersen Hansen et al. from Norway detected the time and phase by locking equalization technology and obtained a high precision of phase values. In 2008, the circular track calibration proposed by Chen et al. took the fixed target on the seabed as the center of the circle, which weakened the influence of sound speed on the horizontal positioning of the transponder. Different from the general calibration algorithm: Chen et al. used the relationship between the target positioning error caused by the Angle deviation and the tracking ship's running track to estimate the Angle deviation according to the known underwater fixed target position, the circular track with various radii, and the different shapes projected by the results of USBL acoustic positioning in the acoustic coordinate system.

Since the circular track may be distorted in actual work, the calibration accuracy may be reduced. In 2013, Chen et al. proposed that the calibration method of linear track should be adopted by the measuring ship when the seabed target is fixed.

(2) Research status of USBL installation error calibration technology in China

At the same time, a series of national research programs, such as "863", attach great importance to the study of USBL system. In 2005, Tang Qiuhua and Wu Yongting et al. explicitly proposed the calibration algorithm of USBL for the first time in China. This idea is similar to but different from Jan's method, which equates installation calibration to parameter estimation problem, uses optimization method to estimate components of installation displacement deviation and installation rotation deviation, and obtains each magnitude value based on least squares. In the same year, Yu Min from Harbin Engineering University used this method to improve the numerical method and proposed a robust algorithm for the development of long range ultra-short baselines. It is mainly applicable to the calibration in shallow sea conditions, and the data is obtained by sailing around the ship, and the better positioning results are obtained. In this paper, we use the observation equation proposed by Wu Yongting and improve the calibration algorithm, and further study the iterative least squares, robust estimation algorithm and sequential least squares.

In 2006, Yansuo Liu et al proposed a nonlinear iterative algorithm to calculate location installation deviations. This algorithm provides a solution, but it inevitably leads to low estimation accuracy and scatter results in underwater work. In the same year ** set up the Institute of Physics and Undersea Technology of the School of Applied Oceanography in the Asia-Pacific Research Center of Sun Yat-sen University, and gave another calibration algorithm. This algorithm is based on the three-dimensional positioning error under the influence of rotation Angle and geometric diagram method. It also requires the underwater target to have a trackable motion, but this algorithm is not applicable to the domestic system. In 2007, Zheng Cuie from Harbin Engineering University discussed the calibration of USBL installation on the underwater platform of USBL, cited the calibration observation equation, and included the influence factors of sound line bending. His research adopts two steps to calibrate the observation equation. One is to keep the equation unchanged, the other is to set the observation quantity as the incident Angle between the acoustic line and the matrix. The problem of line selection was her first, and the circular track was taken as an example to illustrate the positioning under the influence of installation rotation error.

In 2010, Yang Baoguo analyzed the observation model of Angle deviation and compared a variety of calculation methods for Angle deviation calibration. In 2013, Li Zhao et al. analyzed the influence of sound velocity error on calibration and proposed the idea of combining circle and straight line in calibration track.

V. Conclusion

In this paper, several methods to calibrate the positioning error of ultra short baseline underwater acoustic positioning system are reviewed. At present, foreign countries have made remarkable research achievements in the ultra short baseline positioning system, which is an underwater positioning equipment. China also attaches more and more importance to the research of underwater positioning technology, and gradually speeds up the pace of research in this field. It is not difficult to find that there are many factors affecting the positioning accuracy of the ultra-short baseline. Future research can be carried out from various aspects, such as the comprehensive consideration of the array error, acoustic line bending and installation error of the USBL, so as to maximize the positioning accuracy of the ultra-short baseline.

References:

[1] ZHENG Cuie, SUN Dajun, ZHANG Dianlun, LI Xiang. Research on Installation Error Calibration Technology of Ultra Short Baseline Positioning System [J]. Computer Engineering and Applications, 2007 (08) : 171-173.

[2] ZHANG Tongwei, WANG Xiangxin, TANG Jialing, QIN Shengjie. Status and Prospect of Ultra-short baseline positioning system in deep sea [J]. Ship Electronic Engineering, 2018,38 (10) : 1-6.

[3] SUN Dajun, ZHENG Cuie, ZHANG Jucheng, HAN Yunfeng, CUI Hongyu. Development and Prospect of underwater acoustic Positioning and navigation Technology [J]. Bulletin of Chinese Academy of Sciences, 2019, 34 (03) : 331-338.

[4] YU Min. Development of Long-Range Ultra-Short Baseline Positioning System [D]. Harbin: Harbin Engineering University, 2005.

[5] Liu Nian, Yue Xianchang, Li Yuhuan, Yi Xianzhou. Based on Automatic recognition system